Linear Regression

[Linear Regression]

Regression(회귀)는 지도학습에 포함되는 방법론입니다. 그 중에서도 Linear Regression을 알아볼텐데요.

Linear은 "선형"이라는 뜻을 가지고 있습니다. 선형이라 함은 배수로 늘어나는 값을 가진 것들의 모양세를 말합니다.

그래프로 표현하면 기울기를 가지고 있는 직선으로 표현됩니다.

즉, Linear Regression은 배수로 늘어나는 연속적인 값들의 데이터로 예측하는 것입니다.

값을 예측하기 전에 가설을 세울 필요가 있습니다.

Linear Regression의 경우 "이 데이터들은 배수로 늘어나는 연속적인 값들의 데이터이기 때문에 이를 만족하는 1차 함수가 있을 것이다"라는 가설입니다. 그리고 그 1차 함수를 Hypothesis라고 합니다. (Linear가 아닐 경우에는 다양한 함수가 Hypothesis가 되겠죠)

[그림1] Hypothesis의 모습은 학습의 과정을 통해 2번(정답)을 향해 간다.

자, 여기서 목표는 Hypothesis를 하나의 정답(하나의 직선)으로 추론해나가는 것이고 그 과정은 우리가 아닌 기계가 할 것입니다!

이게 Machine Learning의 과정입니다.

Hypothesis를 수식으로 표현 해보겠습니다.

기울기가 존재하는 1차 함수입니다.

Hypothesis의 모습은 W (weight)와 b (bias)에 따라 달라질 겁니다.

그렇다면 W와 b를 찾아야 할텐데요. 어떻게 찾아야 하는지 생각해봅시다.

[그림2] 가상의 선(Hypothesis)와 실제 데이터 값의 차이를 이용하자!

정답을 주고 학습을 시키는 지도학습의 특징이 여기서 나타납니다. 정답들과 Hypothesis의 차이가 가장 적은 것이 찾고자 하는 직선이 되겠죠.

여기서 Cost Function을 소개하겠습니다.

Cost Function은 우리가 세운 가설(Hypothesis)와 실제 정답과 차이가 얼마나 심한지 알려줍니다.

이해를 돕기 위해 [그림2]의 Cost Function이 도출되는 과정을 살펴보겠습니다.

우리가 예측하는 값(H(x))과 실제 정답(y)와의 차이의 제곱들의 합이 Cost값이 됩니다.

(제곱들의 합인 이유는 차이가 크면 Cost값이 확 늘어나고, 차이가 적으면 Cost값이 확 줄어들기 때문에 효율적입니다)

정리! 우리가 세운 가설과 정답의 차이가 Cost Function입니다.

그렇다면 Cost Function이 작은 것이 좋겠군요.

그렇습니다. 기계학습은 Cost Function이 가장 작은 값을 찾는 과정입니다.

즉, 주어진 "연속적인 데이터"를 통해 다른 데이터를 예측하는 기계학습(Linear Regression)을 위해서는 알맞는 Hypothesis를 찾아야 합니다.

그 Hypothesis를 찾으려면 W(weight)와 b(bias)가 Cost Function을 통해 나온 Cost값이 작아지는 방향으로 변해야 합니다.

import tensorflow as tf

import matplotlib.pyplot as plt

x = [1,2,3]

y = [1,2,3]

W = tf.Variable(tf.random_number([1]), name = 'weight')

b = tf.Variable(tf.random_number([1]), name = 'bias')

hypothesis = x * W + b

cost = tf.reduce_mean(tf.square(hypothesis-y))

자, 이제 개념정리를 열심히 했으니, 신나게 코딩할 시간입니다.

위의 코드는 1일 때 1, 2일 때 2, 3일 때 3인 값이 나오는 Linear한 결과값들입니다.

이 결과값들로 지도학습의 Regression 방법론을 사용할 겁니다.

x와 y라는 변수에 [1, 2, 3]의 list를 추가하고 Weight와 Bias를 설정합니다.

Weight와 Bias는 학습하면서 값이 바뀝니다. 그렇기 때문에 tf.Variable이라는 텐서플로우 메소드를 사용해서 변수를 지정해줍니다. 주로 random값으로 시작하기 때문에 1개 요소의 random값을 부여해줍니다.

hypothesis는 우리가 위에서 배운대로 수식을 사용하면 되고

cost는 reduce_mean(평균) 과 square 메소드를 통해 쉽게 표현할 수 있습니다.

이제 cost값이 줄어드는 방향으로 이동해야겠죠?

어려울 것 같지만 걱정하지마세요. 우리들이 python 모듈을 사용하는데에는 다 이유가 있습니다.

## Reduce Cost

optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)

train = optimizer.minimize(cost)

sess = tf.Session()

## tf.Variable을 사용하기 위해서는 초기화가 필수적이다.

sess.run(tf.global_variables_initializer())

for step in range(2001):

sess.run(train)

if step % 20 == 0:

print(step, sess.run(cost), sess.run(W), sess.run(b))

train 메소드의 GradientDescentOptimizer을 사용하면 미분값을 Optimize하게 되고 (미분값을 구하는 이유는 나중에 설명하도록 하겠습니다) minimize 메소드를 사용하면 미분값이 줄어드는 방향으로 움직이게 됩니다.

이 과정을 반복문을 통해 반복시키면 Cost값이 줄어드는 과정을 확인할 수 있습니다.

그리고 원하는 W와 b (딱히 계산해보지 않아도 우리는 답이 W = 1, b = 0 임을 알 수 있습니다)를 확인할 수 있죠.

[전체코드]

import tensorflow as tf

x = [1,2,3]

y = [1,2,3]

W = tf.Variable(tf.random_normal([1]), name = 'weight')

b = tf.Variable(tf.random_normal([1]), name = 'bias')

hypothesis = x * W + b

cost = tf.reduce_mean(tf.square(hypothesis-y))

## Reduce Cost

optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)

train = optimizer.minimize(cost)

sess = tf.Session()

## tf.Variable을 사용하기 위해서는 초기화가 필수적이다.

sess.run(tf.global_variables_initializer())

for step in range(2001):

sess.run(train)

if step % 20 == 0:

print(step, sess.run(cost), sess.run(W), sess.run(b))

[Output]

0 14.762665 [-1.2744149] [1.1851974]

20 0.56644654 [0.09239645] [1.6837394]

40 0.39802802 [0.2550194] [1.6573844]

60 0.36043978 [0.30145413] [1.5845186]

80 0.3273476 [0.3353709] [1.5105306]

100 0.29730222 [0.3667096] [1.4395868]

120 0.27001464 [0.39648175] [1.3719358]

140 0.24523152 [0.42484593] [1.3074601]

...

...

...

1840 6.849395e-05 [0.9903878] [0.02185074]

1860 6.220707e-05 [0.99083954] [0.02082383]

1880 5.649686e-05 [0.9912701] [0.01984516]

1900 5.131116e-05 [0.9916804] [0.01891248]

1920 4.660153e-05 [0.9920714] [0.01802365]

1940 4.2325366e-05 [0.9924439] [0.01717661]

1960 3.8440172e-05 [0.9927991] [0.01636939]

1980 3.4911765e-05 [0.9931375] [0.01560006]

2000 3.170744e-05 [0.99346] [0.01486693]

[참고]

placeholder를 이용해서 코드를 작성하면 machine을 틀만 만들어서 도구처럼 만들어 놓은 뒤 train sample을 집어넣으면 그때그때 결과값을 얻을 수 있습니다.

1 2 3 4 5 6 7

x = tf.placeholder(tf.float32, shape = [None]) ## shape은 N차원 텐서를 뜻하는 말로 아무차원의 값을 입력받을 수 있다. y = tf.placeholder(tf.float32, shaple = [None])   for step in range(2001):     cost_val, W_val, b_val, _ = sess.run([cost, W, b, train], feed_dict = { x : [1, 2, 3, 4, 5], b : [2.1, 3.1, 4.1, 5.1, 6.1]})     if step%20 == 0:         print(step, cost_val, W_val, b_val) Colored by Color Scripter

cs

x, y를 placeholder로 지정,

cost_val = sess.run(cost)

W_val = sess.run(W)

b_val = sess.run(b)

에 대응되고 x와 y 값에는 주어진 벡터를 넣는 script로 구성합니다.

[Cost Function]

Cost Function은 어떻게 생겼을까. 그리고 cost값을 minimize하는 과정은 어떻게 일어나는지 궁금합니다.

Cost Function은 어떻게 생겼는지 궁금하면, 간단합니다! 직접 그려보죠. 

Cost Function이 어떻게 생겼는지 보기 위해서 minimize하지 않고 전체의 형태를 보겠습니다.

import tensorflow as tf

import matplotlib ## matplot 설치후 lib 사용

matplotlib.use('TKAgg') ## 사용 오류시 matplot의 backend를 지정해준다. 서버에 Graph를 띄울 것인지, 그냥 사진으로 띄울것인지 상수로 정해주는 작업

import matplotlib.pyplot as plt

x = [1,2,3]

y = [1,2,3]

W = tf.placeholder(tf.float32) ## W의 값을 점차적으로 증가시킴에 따라 그래프를 그려야 하므로 빈공간으로 선언한다.

hypothesis = x * W

cost = tf.reduce_mean(tf.square(hypothesis-y))

sess = tf.Session()

sess.run(tf.global_variables_initializer())

W_val = [] ## W값을 배열로 저장한 후 Graph로 띄워야 한다.

cost_val = []

for i in range(-30, 50):

feed_W = i*0.1

curr_cost, curr_W = sess.run([cost,W], feed_dict = {W: feed_W}) ## x축이 되는 W의 범위를 cost func에 넣는다. (feed_dict)

W_val.append(curr_W) ## 배열에 추가

cost_val.append(curr_cost) ## 배열에 추가

plt.plot(W_val, cost_val) ## curr_W 배열에 저장된 모든 값을 그래프로 그린다. (x축 W_val, y축 cost_val)

plt.show() ## 그래프를 실행한다.

[그림3] 우리가 찾는 점은 cost가 0인 부분. W가 1이다. (b는 생략하고 그림. b와 함께 그리면 3차원으로 표현된다)

Weight에 따른 Cost Function은 2차원 그래프로 그려집니다. (2차식)

Cost가 가장 작은 값을 찾아가는 과정을 Minimize 하는 과정이라고 하죠.

수학적으로 그래프의 최소값을 찾으려면 기울기가 0인 지점을 찾아야 합니다. ( (m>0)이고 제곱식이므로 무조건 최소값이 존재한다. 잊으셨다면 수학의 정석 뒤적뒤적..)

Weight과 Cost 함수를 1차 미분하면 기울기가 0인 지점을 찾을 수 있습니다. 

여기까지는 사람이 직접 최소값을 찾기 위한 과정이고, 이제 컴퓨터에게 시킬 차례입니다. 우리가 직접 알려주지 않아도 됩니다. 컴퓨터는 이미 알고 있습니다.

Gradient Decent Algorithm라는 것으로 기계는 가장 작은 Cost 값을 찾을 수 있습니다.

이 알고리즘이 들어간 메소드가 위 코드에서 나온 tf.train.GradientDecentOptimizer.minimize() 입니다.

Gradient Decent Algorithm은 원래 W에서 Cost Function을 W로 미분한 값을 빼주면서 이동합니다.

여기서 는 learning rate(학습계수)입니다.

학습계수가 높으면 조금더 성큼성큼 움직이며 최소 Cost값을 찾겠죠.

하지만 너무 크면 계속 최소 Cost값을 찾지 못하고 그 사이를 넘어다니므로 적당한 learning rate가 필요합니다.

(이는 어떤 학습 데이터를 사용하느냐에 따라 크게 좌우됩니다.)

[Convex Function]

b (Bias)값이 있을 경우에는 그래프가 3차원으로 나오게 됩니다.

x = Weight, y = bias, z = cost 인 그래프가 아래와 같이 나온다고 생각해보죠.

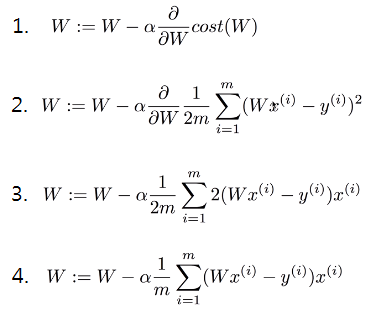
[그림4] 이런 형태의 Cost Function이면 대.략.난.감.

기울기가 작아지는 쪽으로만 이동하는 Gradient Decent Algorithm은 [그림4]와 같은 Cost Function에서 효과를 보지 못합니다. 하나의 웅덩이에 빠지면 다른 곳으로 이동하지 못하기 때문에 그 점이 최소 Cost인지 알지 못하죠.

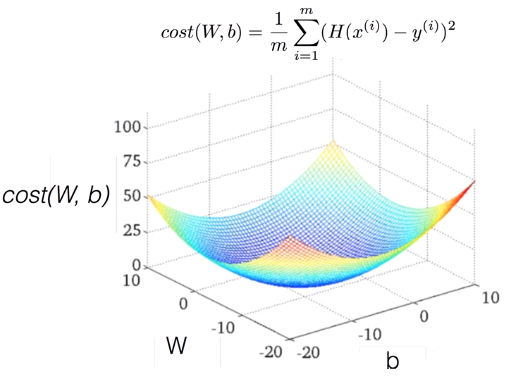
[그림5] 우리는 이런 Cost Function을 원한다!

그래서 우리는 검증이 필요합니다. [그림5]와 같은 Cost Function을 가지는지 확인할 필요가 있죠.

이를 Convex Function이라고 합니다.

Cost Function이 Convex Function일 때, 우리는 Gradient Decent Algorithm을 사용할 수 있습니다.